Skip to content

100. Same Tree

Easy

Description

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

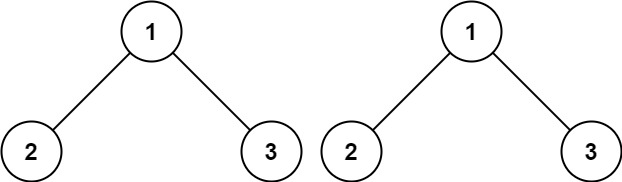
Example 1:

Input: p = [1,2,3], q = [1,2,3]
Output: true

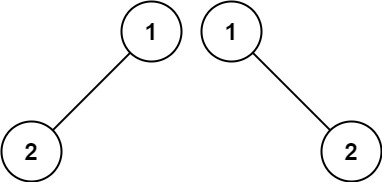
Example_1_img

Example 2:

Input: p = [1,2], q = [1,null,2]
Output: false

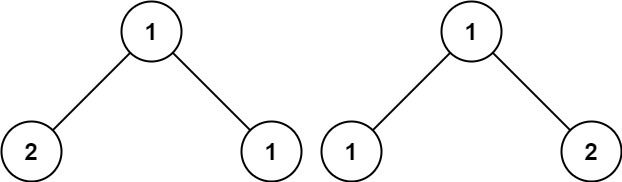
Example_1_img

Example 3:

Input: p = [1,2,1], q = [1,1,2]
Output: false

Example_1_img

Constraints:

  • The number of nodes in both trees is in the range [0, 100].
  • -10โด <= Node.val <= 10โด

Solutions ๐Ÿ”’

Approach: DFS

Time complexity: \(O(min(m,n))\)

Space complexity: \(O(min(m,n))\)

Algorithm

We can use the DFS recursive method to solve this problem.

  • First, determine whether the root nodes of the two binary trees are the same.
  • If both root nodes are null, then the two binary trees are the same.
  • If only one of the root nodes is null, then the two binary trees are definitely different.
  • If both root nodes are not null, then determine whether their values are the same.
  • If they are not the same, then the two binary trees are definitely different.
  • If they are the same, then determine whether the left subtrees of the two binary trees are the same and whether the right subtrees are the same.

The two binary trees are the same only when all the above conditions are met.

The time complexity is \(O(min(m,n))\), and the space complexity is \(O(min(m,n))\). Here, \(m\) and \(n\) are the number of nodes in the two binary trees, respectively.

The space complexity mainly depends on the number of layers of recursive calls, which will not exceed the number of nodes in the smaller binary tree.

Way 1:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if p==q:                                                                        #Step 3
            return True
        if not p or not q or p.val!=q.val:                                              #Step 2
            return False
        return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)      #Step 1

Way 2 : Another way of writing DFS

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if not p and not q:
            return True
        if not p or not q:
            return False
        if p.val!=q.val:
            return False
        return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)

Way 3 : Another way of writing DFS

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if not p or not q:
            return p==q # covers: p=none and q!=none, q=none and p!=none, both none
        return p.val==q.val and self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)

Stick to DFS appraoch

Akhil Singh Chauhan Akhil Singh Chauhan
Creator

Comments