240. Search a 2D Matrix II
Medium
Description
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
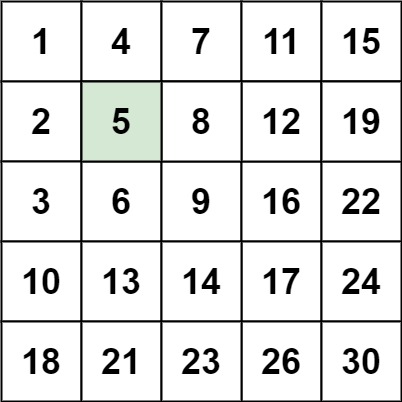
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Example 2:
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109All the integers in each row are sorted in ascending order.All the integers in each column are sorted in ascending order.-109 <= target <= 109
Solutions
Approach : Search from the Bottom Left or Top Right
Time complexity: \(O(m + n)\)
Space complexity: \(O(1)\)
Algorithmic
Here, we start searching from the bottom-left and move towards the top-right direction. We compare the current element \(\textit{matrix}[row][col]\) with \(\textit{target}\):
- If \(\textit{matrix}[row][col] = \textit{target}\), it means the target value is found, and we return \(\text{true}\).
- If \(\textit{matrix}[row][col] > \textit{target}\), it means all elements in this column from the current position upwards are greater than \(\textit{target}\), so we move the \(row\) pointer upwards, i.e., \(row \leftarrow row - 1\).
- If \(\textit{matrix}[row][col] < \textit{target}\), it means all elements in this row from the current position to the right are less than \(\textit{target}\), so we move the \(col\) pointer to the right, i.e., \(col \leftarrow col + 1\).
If the search ends and the \(\textit{target}\) is not found, return \(\text{false}\).
The time complexity is \(O(m + n)\), where \(m\) and \(n\) are the number of rows and columns of the matrix, respectively. The space complexity is \(O(1)\).
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if not matrix or not matrix[0]:
return False
m , n = len(matrix) , len(matrix[0])
row = m-1
col = 0
while row >= 0 and col < n:
if matrix[row][col]==target:
return True
if matrix[row][col] > target:
row -= 1 # all numbers in that row are even larger
else: #matrix[row][col]<target
col += 1 # all numbers in this row from current position col are smaller
return False
Approach : 1D-Binary Search
Time complexity: \(O(m \log(n))\)
Space complexity: \(O(1)\)
Way 1
Algorithmic
- Applicable to searching target in a 2D row-wise sorted matrix
Since all elements in each row are sorted in ascending order, for each row, we can use binary search to find the first element greater than or equal to \(\textit{target}\), and then check if that element is equal to \(\textit{target}\). If it is equal to \(\textit{target}\), it means the target value is found, and we return \(\text{true}\). If it is not equal to \(\textit{target}\), it means all elements in this row are less than \(\textit{target}\), and we should continue searching the next row.
If all rows have been searched and the target value is not found, it means the target value does not exist, and we return \(\text{false}\).
The time complexity is \(O(m \times \log n)\), where \(m\) and \(n\) are the number of rows and columns of the matrix, respectively. The space complexity is \(O(1)\).
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
def binarySearch(arr, target):
l, r = 0, len(arr) - 1
while l <= r:
mid = (r+l)//2
if arr[mid]==target:
return True
if arr[mid]>target:
r=mid-1
else:
l=mid+1
return False
for arr in matrix:
if binarySearch(arr, target):
return True
return False
equivalency
Way2
Pythonic
Access to detailed solutions requires a login. Already have an account? Don't have an account yet?
👋 Please log in to view the solution
Akhil Singh Chauhan
Author