52. N-Queens II
Hard
Description
The n-queens puzzle is the problem of placing \(n\) queens on an \(n \times n\) chessboard such that no two queens attack each other.
Given an integer \(n\), return the number of distinct solutions to the n-queens puzzle.
Example 1:
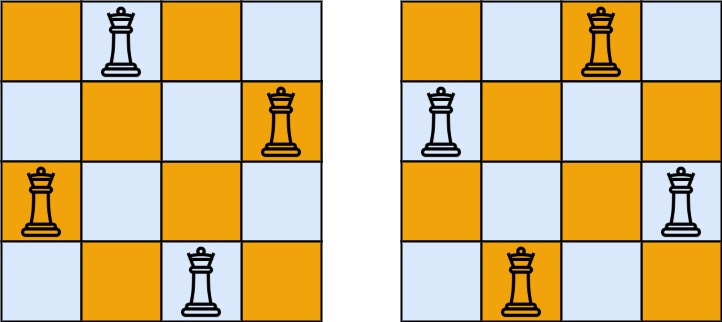
Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown below
Example 2:
Constraints:
1 <= n <= 9
Solutions
Video Solution Coming Soon
Approach : Backtracking
Time complexity: \(O(n!)\)
Space complexity: \(O(n)\)
Way 1
Algorithmic
The problem requires us to find all distinct ways to place n queens on an \(n \times n\) chessboard so that no two queens threaten each other.
We use a backtracking depth-first search (DFS) approach to explore all possible placements of queens row by row.
To efficiently check if a queen can be placed at position \((i, j)\), we keep track of columns, diagonals, and anti-diagonals that are already occupied by queens using three boolean arrays.
For each column \(j\) in row \(i\), we calculate the diagonal index (d_idx) and anti-diagonal index (ad_idx). If any of these positions are already marked as True in their respective arrays, we skip placing a queen there.
If a queen can be placed, we mark the column, diagonal, and anti-diagonal as True and recursively attempt to place queens in the next row.
After exploring all possibilities for the current row, we backtrack by marking the column, diagonal, and anti-diagonal as False, allowing other potential placements to be explored.
The base case for our DFS function is when i equals n, which means we have successfully placed \(n\) queens without conflicts, and we increment the answer counter.
class Solution:
def totalNQueens(self, n: int) -> int:
def dfs(i: int) -> None:
nonlocal ans
if i == n:
ans += 1
return
for j in range(n):
d_idx, ad_idx = i + j , j - i + n - 1
if cols[j] or diag[d_idx] or a_diag[ad_idx]:
continue
cols[j] = diag[d_idx] = a_diag[ad_idx] = True
dfs(i + 1)
cols[j] = diag[d_idx] = a_diag[ad_idx] = False
#initialization
ans = 0
cols = [False] * n
diag = [False] * (2 * n - 1)
a_diag = [False] * (2 * n - 1)
dfs(0) #dfs start
return ans
Detailed Complexity Discussion
The time complexity of this solution is \(O(n!)\) in the worst case. This is because we attempt to place a queen in each column of each row, and once a queen is placed, we reduce the problem size by one row. In the best case, where conflicts occur early, it can be less than \(O(n!)\). However, on average, the algorithm explores a significant portion of the n! possible permutations of queen placements.
The space complexity is \(O(n)\) due to the storage required for the three boolean arrays (cols, diag, a_diag) that track the columns, diagonals, and anti-diagonals respectively. These arrays have sizes \(n\), \(2n-1\), and \(2n-1\), all of which are proportional to \(n\). Additionally, the recursion stack can go up to a depth of \(n\), contributing to the space complexity.
Access to detailed solutions requires a login. Already have an account? Don't have an account yet?
👋 Please log in to view the solution
Akhil Singh Chauhan
Author