74. Search a 2D Matrix
Medium
Description
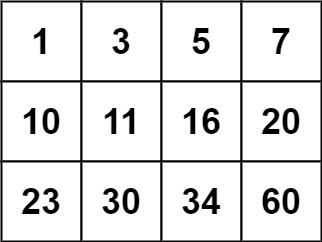
You are given an m x n integer matrix matrix with the following two properties:
- Each row is sorted in non-decreasing order.
- The first integer of each row is greater than the last integer of the previous row.
- Given an integer target, return true if target is in matrix or false otherwise.
You must write a solution in O(log(m * n)) time complexity.
Example 1:
Example 2:
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
Solutions
Video Solution Coming Soon
Approach : (Optimised) Binary Search in a 2D Matrix
Time complexity: \(O(log(m \times n))\)
Space complexity: \(O(1)\)
Way 1
Algorithmic
The given matrix has special properties where each row is sorted and the first element of each row is greater than the last element of the previous row.
This means that matrix is sorted if you go from top left to bottom right, row by row. So we can treat this 2D matrix as a sorted 1D array and use Binary Search to find the target.
The key is to convert the middle index of binary search into corresponding row and column indices of the matrix.
To convert a 1D index to 2D indices, we can use:
-
row = index / number of columns
-
column = index % number of columns
The time complexity of this solution is O(log(m * n)) as we are performing binary search on m * n elements.
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
#Get Dimensions
m , n = len(matrix),len(matrix[0])
#Initialize BS boundaries
left ,right = 0 , m*n
#Start Search
while left<right:
#crucial steps
mid = (left+right)//2
# Convert 1D index to 2D indices
i , j = mid//n, mid % n #To get the row and column of the midpoint in the matrix
# Compare current element with target
if matrix[i][j]==target:
return True
if matrix[i][j]<target:
left= mid+1
else:
right= mid
return False
Way 2
Another way of writing Binary Search
We can logically unfold the two-dimensional matrix and then perform binary search. The time complexity is O (log(m x n)), where m and n are the number of rows and columns of the matrix, respectively. The space complexity is O (1).
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m , n = len(matrix), len(matrix[0])
left, right = 0, m*n-1
while left<=right:
mid = (left+right)>>1
i, j = divmod(mid,n) # note: divide column count
if matrix[i][j]==target:
return True
elif matrix[i][j]<target:
left= mid+1
else:
right= mid-1
return False
class Solution {
fun searchMatrix(matrix: Array<IntArray>, target: Int): Boolean {
if (matrix.isEmpty() || matrix[0].isEmpty()) return false
val m = matrix.size
val n = matrix[0].size
var left = 0
var right = m * n - 1
while (left <= right) {
val mid = left + (right - left) / 2
val midValue = matrix[mid / n][mid % n]
when {
midValue == target -> return true
midValue < target -> left = mid + 1
else -> right = mid - 1
}
}
return false
}
}
equivalency
- To get the row and column of the midpoint in the matrix, we use the
divmodfunction with mid and n. Thedivmodfunction takes two numbers and returns a pair of numbers (a tuple) consisting of their quotient and remainder.
Approach : Search from the Bottom Left or Top Right
Time complexity: \(O(m + n))\)
Space complexity: \(O(1)\)
Algorithm2 for general matrix
Here, we start searching from the bottom left corner and move towards the top right direction. We compare the current element matrix[row][col] with target:
- If matrix [row][col] = target, we have found the target value and return true.
- If matrix [row][col] > target, all elements to the right of the current position in this row are greater than target, so we should move the pointer row upwards/left, i.e., row = row — 1.
- If matrix[row][col] < target, all elements above the current position in this column are less than target, so we should move the pointer col to the right, i.e., col = col+ 1.
- If we still cant find target after the search, return false.
The time complexity is O(m + n), where m and n are the number of rows and columns of the matrix, respectively. The space complexity is O (1).
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if not matrix or not matrix[0]:
return False
m , n = len(matrix),len(matrix[0])
row , col = m-1,0
while row>=0 and col<n:
if matrix[row][col] == target:
return True
elif matrix[row][col]>target:
row-=1
else: #matrix[row][col]<target
col+=1
return False
Approach : 1D-Binary Search
Time complexity: \(O(m \log(n))\)
Space complexity: \(O(1)\)
Algorithm3
- Applicable to searching target in any 2D matrix
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
def BinarySearch(arr, target) -> bool:
l , r = 0, len(arr)
while l<r:
mid = (l+r)//2
if arr[mid]>target:
r=mid
elif arr[mid]<target:
l = mid+1
else:
return True
return False
for arr in matrix:
if BinarySearch(arr,target):
return True
return False
Access to detailed solutions requires a login. Already have an account? Don't have an account yet?
👋 Please log in to view the solution
Akhil Singh Chauhan
Author